古川准教授

Special Interview 2
数学(純粋数学)分野
代数幾何学専門 古川 勝久 准教授
数学(純粋数学)分野
代数幾何学専門 古川 勝久 准教授
目に見えない高次元の図形を、代数を用いて考える
――古川先生は高校時代、やっぱり数学が得意でしたか?

「物理」もけっこう勉強していましたね。物理と数学は相性がいいから。ただ、物理でも数式は使いますが、その用法は割とおおざっぱ(笑)。もう少し機密にやってみたいと大学では数学を選びました。もうひとつ、「高次元の幾何学」に興味を持ったのも現代数学に魅かれた理由です。
――高次元の幾何学……。勝手なイメージですが、数学が好きな中高生は「素数」を好む、という印象があります。

確かに素数を通して代数に魅力を感じる学生は多いですね。素数は基本になるものだから、本能的に好きになるのかな。専門的にいうと、整数の剰余環という数の体系を作るときに「割る数」としてうまく機能し、良い体系を与えるにはやはり素数です。大学では代数学基礎という授業で『初等整数論』を扱いますが、そこでも素数はかなり重要ですね。
――古川先生のご研究は代数幾何学の領域だそうですか、高次元の幾何学というのは???

4次元以上の幾何学を高次元幾何学といいます。4次元の図形ってどんなものか、想像することすらできないでしょう?目に見えないものをどうやって研究するんだという話ですが、そこで多項式を用いてるわけです。多項式を考えるのは代数です。
――つながっているんですね!
【FOCUS】多変数の多項式をアルゴリズムによって計算する
セミナーでは発展的内容として、多項式によって定義された高次元における代数多様体の幾何学を探求しています。その前段として代数・アルゴリズムによる多項式論や、それを扱う可換環の理論を学んでいきます。高次元の多項式とは、簡単にいうと「X1,...,Xn」といった多変数で考えますが、その分析には様々な方法があり、私がひとつ用いているのが、多変数の多項式を順序づけ、アルゴリズムによって計算する「グレブナ基底」という概念です。多変数多項式の割り算も含めて、これらは数学におけるさまざまな計算を可能にするのはもとより、工学などを含めたあらゆる分野に広く応用の道を開く理論研究です。
――う~ん、難しい……。多項式と図形の例として、多項式によって定義された代数多様体について教えてください。

代数多様体とは「多項式=0」で定義される図形です。例えば、2変数の式「xy=1」だと、次のような双曲線になりますね。
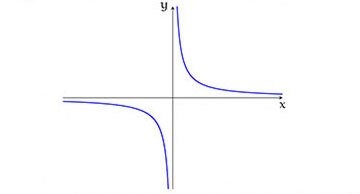

「xy=1」は、「xy-1=0」と書いても同じことなので、この図形は、V(xy-1)={(x,y)∈R2|xy-1=0}のように集合として表せます
――なるほど。

これが多変数の多項式たどf1,...fr∈R[X1,...,Xn]に対して、V(f1,...fr)={(X1,...Xn)∈Rn|f1(X1,...,Xn)=・・・=fr(X1,...,Xn)=0}によって、専門的にいうとアフィン代数多様体が定義されます。
すると、例えば2つの多項式「X-1」と「y-1∈k[x,y]」について、V(x-1,y-1)={(x,y)∈Rn|x-1=y-1=0}={(1,1)}が求められます。
したがって先の図形は、
▶双曲線 V(xy-1).
▶点(1,1)=V(x-1,y-1).
▶x軸=V(y),y軸=V(x).
▶双曲線 V(xy-1).
▶点(1,1)=V(x-1,y-1).
▶x軸=V(y),y軸=V(x).
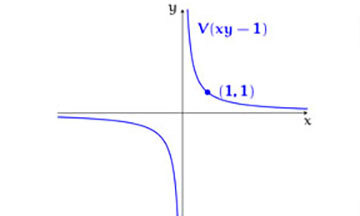

このように、点・直線・曲線などの図形が、多項式を使うとV(f1,...,fr)で表せるのです。
――いろいろな図形が数式で表現できるんですね!
【FOCUS】高校数学と大学数学の違いって?
多変数多項式のつくる図形は、大学4年生のセミナーのテーマなので、高校生のみなさんには手強かったかもしれません。でも段階を踏んで学べば、充分に理解できるようになります。そのためにも数学の勉強は、基本的なところからゆっくりと、着実に習得することが肝心です。大学数学の入口として代表的なのが、授業科目でいえば「数学序論」です。この科目では高校の「数III」の内容も復習しますが、大学の授業ですから、数IIIでは曖昧になっていた部分もしっかりと学びます。
――曖昧な部分とは?

例えば、解析では「(an)n∈N」など、「n」を無限に大きくする記号がありますが、「無限に近づける」というと、一般的には抽象的な表現でしょう?
――そうですね。詩的な感じがします。

数列では「無限大に発散する」「極限に収束する」などの言い方をしますが、現代数学では、この「無限」や「発散」、「収束」といった言葉一つひとつに明確な定義があります。
しかし高校の数学では、そこまでは数えません。高校数学は誰でも理解できるように設計されていますから、そこは習慣的にわかっているものとしてスルーします。いわゆるブラックボックスですね。
しかし高校の数学では、そこまでは数えません。高校数学は誰でも理解できるように設計されていますから、そこは習慣的にわかっているものとしてスルーします。いわゆるブラックボックスですね。
――大学数学ではブラックボックスの中にも光を当てる。

その点がひとつ高校数学との違いです。また1年次では「フレッシュマンセミナー」という授業の特色です。
数学を研究する上でかならず必要となる集合論を学ぶほか、数学における文章の書き方や、論理的な思考法をトレーニングします。
数学を研究する上でかならず必要となる集合論を学ぶほか、数学における文章の書き方や、論理的な思考法をトレーニングします。
――ロジカルシンキングですね。社会に出て役立つ力のひとつです。

世の中に起きる問題って、政治や経済など複雑な要素がいろいろと絡み合っていて、整理するのが難しいですよね。最初からカオスの状況の中で物事を考える訓練をするのはハードルが高いんじゃないかな。
その点、数学は前提条件が明確・厳密なので、筋道を立てて物事を考える訓練としても入りやすいと思います。
その点、数学は前提条件が明確・厳密なので、筋道を立てて物事を考える訓練としても入りやすいと思います。
――大学では数学的な思考力を鍛えつつ。研究でやってみたい分野を見つけるんですね。

学年が上がると、だんだん選択科目が増えていきます。数学の特徴は勉強に取り組むなかで、「自分に向いている・向いていない」という傾向が、非常に強く出てくることです。しかし数学は分野が広いので、例えば自分は解析が苦手で代数が得意だとわかれば、代数に力を入れればOK。すべて完璧にマスターするのは難しいので、そこは柔軟に考えて構いません。セミナーを選択する頃までには、自分の「得意」が見えてくるはずです。
決して色あせない学問を、仲間とともに学ぶ
――古川先生にとって純粋数学の魅力とは何ですか?

研究成果を上げるのはなかなか難しいですが、それだけに結果を出して論文にまとまったときの達成感は大きいですね。
また、その結果が永続的に失われないことも純粋数学の魅力です。例えば論文を書く際に、参考文献として100年前の論文でも普通に引用できるのは、他の学問分野では珍しいでしょう。変化の激しい世の中にあっても、失われることが少ないのです。
また、その結果が永続的に失われないことも純粋数学の魅力です。例えば論文を書く際に、参考文献として100年前の論文でも普通に引用できるのは、他の学問分野では珍しいでしょう。変化の激しい世の中にあっても、失われることが少ないのです。
――確かに堅牢な学問と言えますね。数学科の学生さんにはどんなタイプが多いのでしょうか?

坂戸キャンパスでは、中学・高校の数学の先生を目指す人が多いかな。おおよそ8割の学生が入学時点では教員志望です。教師になりたい、という思いが一番の人と、数学が好きだから数学の先生になりたいという人が混在している感じです。もちろん教員になるためのサポート体制はしっかりしていて、3年の授業では数え方を学ぶアドヴァンストセミナーもあります。高校数学が得意な先生が講師を務めています。
――実際の就職先はどんな感じでしょう?

私は2020年に着任して、まだ卒業生を送り出していないのでセミナー生の進路実績はこれからですが、教員免許を取得するのは6割、先生になるのは2~3割と聞いています。あとは企業への就職が中心で、学ぶうちに「企業で働くのも面白そう!」と視野を広げる学生が確かに増えていると感じています。社会はいま科学的な根拠を求めるなど、ますます数学的に動いているので、活躍の場の広がっています。
――坂戸キャンパスの特色はどんなところですか。

坂戸キャンパスだけではなく、城西大学での特色だと思いますが、少人数授業が中心のところです。大学の講義って大教室え行うイメージがあるでしょう?
事実、私がこれまで教えた大学では、学生100人に講義するのが普通でした。でも城西大学は多くても30人クラスだから、先生にも質問もしやすいし、学生同士のコミュニケーションも取りやすいです。
事実、私がこれまで教えた大学では、学生100人に講義するのが普通でした。でも城西大学は多くても30人クラスだから、先生にも質問もしやすいし、学生同士のコミュニケーションも取りやすいです。
――数学だと、オンライン授業でもいけるんじゃないですか?

それは大きな誤解ですよ!私はむしろ、数学こそリアルな対面授業が重要と考えています。城西大学ではひとつの科目がだいたい講義と演習のセットになっていて、演習ではみんなで問題を解きあいます。これが数学を学ぶ上ではかなり大切で、特に演習では先生より、視点を同じくする”発展途上”の学生同士が教え合い、講義を交わすことでグングン伸びていきます。
坂戸キャンパスは自然豊かで、密になりにくい環境にも恵まれていますので、ぜひたくさんの”仲間”と切磋琢磨(せっさたくま)しながら、深淵かつ面白い、数学の世界に分け入ってほしいですね!
次のページ >>
応用数学・コンピュータ科学分野
数値流体力学専門 藤田昌大教授
page 1 2 3
応用数学・コンピュータ科学分野
数値流体力学専門 藤田昌大教授
page 1 2 3



